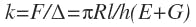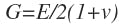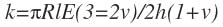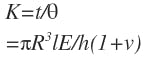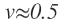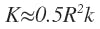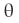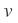How to Calculate the Torsional Stiffness of Rubber Shock Mounts
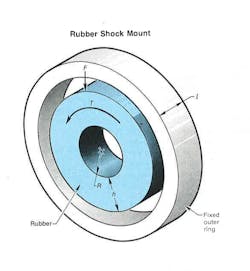
Rubber shock mounts, those simple annularly shaped discs, can cushion shocks and vibrations in the radial and axial directions. Sometimes, however, engineers need to use them to isolate torsional shocks as well. Unfortunately, manufacturers usually only publish the axial and radial spring rates, leaving engineers to guess at the torsional values.
Here is a simple equation that relates the torsional spring rate to the radial spring rate and geometry of the mount.
The radial spring rate for a rubber annular shock mount is:
The modulus of rigidity, G, is:
Therefore:
The torsional spring rate is:
Rearranging the equation for k and substituting in the equation for K yields:
For rubber materials:
Therefore:
This equation gives engineers an accurate estimate of the torsional spring rate of an annular shock mount, one with a radial depth, h, that is not more than 0.1R.
Nomenclature
E = Modulus of elasticity, psi
F = Radial force, lb
G = Modulus of rigidity, psi
H = Radial depth, in.
K = Torsional spring rate, lb-in
k = Radial spring rate, lb-in
l = Rubber thickness, in
R = Rubber inner radius, in
T = Torque, lb-in