This article was updated April 3, 2023. It was originally published June 7, 2016.
RELATED
Structural Properties of Bolted Joints
What’s the Difference Between Bearing, Shear, and Tear-Out Stress?
An Introduction to Lean Bolting
Workers often tighten bolts to 75% to 80% of the bolt proof load. This works for many joints, but in some cases, external tensile loads reduce bolt clamping forces to zero. Something other than the 75% or 80% rule of thumb is needed.
The external tensile force needed to reduce clamping to zero (within the bolt’s and cramped parts’ elastic limits) is determined by:
(Fe/FPR)0 = (Fb/FPR)0
= ((1+r)/r)(Fi/FPR)
where r = Kp/Kb, Kp is the clamped part’s spring constant (lb/in), and Kb is the bolt’s spring constant (lb/in); Fe is the external load on the joint (lb), FPR is the bolt proof load (lb), Fb is bolt load (lb); and Fi is bolt preload (lb). The subscript “0” identifies a value at zero clamping load. This equation can be used to calculate the maximum force that can be applied to a specific joint without the parts separating.
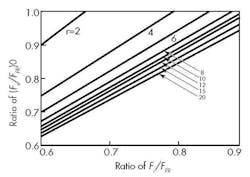
For common values of r, the force can determined from the graph below, which is based on the equation.
The bolt preload that produces a given non-zero clamping force can be determined from the above graph in combination with the equation:
Fe/FPR = (1-b)(Fe/FPR)0
Where b =|Fp/Fi|
The corresponding bolt load can be computed from:
Fb/FPR = (Fe/FPR)0 – Fi/FPR)(b/r)
Here’s an example:
For a bolted joint where r is 10 and Fi/FPR is 0.75, the graph gives:
(Fe/FPR)0 = (Fb/FPR)0
For a clamping force of 25% of the preload (b = 0.25):
(Fe/FPR) = (1-0.25)(0.825)
=0.619
And then:
(Fb/FPR) = 0.825 - (0.75)(0.5)/10
= 0.806