Mechanical resonance, one of the most perplexing problems in motion control, in inherent in most machines.
It usually shows up when you're trying to tune a controller for the first time. What you'll find is that as you raise servo gains bit by bit, perfomrance will gradually improve until a certain point beyond which the machine start making noise. Some machines emit a pure tone, similar to the pitch of a tuning fork.; while other machines "growl" or become unstable, making an unpleasant sound similar to a fog horn.
In a motion system, mechanical resonance is usually caused by compliance or "springiness" between the motor and load. Typically, motors and loads are connected by transmission components such as gear boxes, belts, couplings, and lead screws. Though they may seem stiff, such components actually behave like springs, twisting a little when the motor applies torque. Because it doesn't take much to excite a resonance, this springiness is at the root of many servo problems.
The dyanmic model of a typical motion system is a "two-mass" system (motor and load) connected by a series of springs. Such systems have one frequency where they want to oscillate. Normally, this resonant frequency is well above where the servo controller operates. That is, until you start increasing servo gains.
Resonance worsens with increasing servo gains because higher gains allow the servo controller to reach into higher frequencies. Naturally, if the servo system reaches the resonant frequency, your machine is going to oscillate.
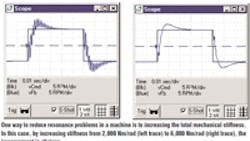
One way to deal with such resonance is to raise the resonant frequency. This usually means "stiffening the springs" by using less compliant components: Instead of compliant helical couplings, use stiffer "bellows" couplings, for example. Instead of long, thin shafts and lead screws, use short, stout ones. If you're using belts, they should be as wide and short as possible, or you can use multiple belts in parallel or special steel or Kevlar-banded belts. Stiffening the frame of your machine isn't a bad idea either.
When there are several "springs" in series, as is the case with most machines, the total spring constant KTotal.
This shows that the most compliant couplings dominate the stiffness. That's why it's important to stiffen the most compliant components. There's little benefit from stiffening the gearbox if the coupling is so compliant that it dominates total spring constant. Fortunately, most vendors of transmission components specify compliance, so looking at the catalog will reduce the guesswork.
Another way to deal with resonance is to reduce the ratio of load-to-motor inertia, making the motor easier to control. Increasing motor inertia is usually the easiest, and sometimes the only, way to improve this ratio. That's because, by the time resonance problems are identified, the machine is designed and the load inertia has, in most cases, been minimized. In general, most servo applications will work well if load inertia is no larger than two times that of the motor.
Increasing motor inertia is no panacea, however, and it can be a real problem in applications requiring fast acceleration/deceleration cycles.
After the mechanical options have been exhausted, it's time to think "electrical." The easiest solution here is to reduce the servo gains. Lowering servo gains, such as the gains of a PI velocity loop, will help resonance. Actually, for a PI (proportional-integral) velocity controller, resonance problems are due almost exclusively to the "P" gain; for PID position loops, they come from the "D" gain.
Although reducing proportional and differential gains eliminates resonance, it also degrades servo performance. The system will respond more slowly to commands, and it won't react as quickly to mechanical disturbances. A better alternative, in most cases, is the use of filters.
Low-pass filters, placed after the velocity loop, often help resonance by limiting the frequency range of the servo controller. The effect is similar to reducing servo gains, but low-pass filters have much less negative impact on servo performance. Be aware, however, that using filters usually causes overshoot, which is something you don't get with mechanical cures.
Shake it up
Ready to explore resonance and its cures for yourself?
The model is pretty flexible, allowing you to adjust stiffness KS load JL and motor JM inertia, low-pass filter frequency LPF, and servo gains for the PI velocity controller KVP and KVI.
Note that increases inertia must be compensated by the use of higher KVP. For example when JM increases by a factor of 11, it doubles the total inertia JM + JL, necessitating a corresponding increase in KVP to maintain servo performance.
Each of the figures in this article can be produced by modifying the model gains according to the following table:
Continue on page 2
Stiff opposition
High mechanical stiffness is the key to speed and precision in machine tools today. By using large diameter lead screws, stiff gearboxes, and strong couplings - all of which contribute to a stiff link between motor and load - machine-tool builders can increase their servo gains without having to worry about instabilities.
Simply put, high servo gains translate to a more valuable machine. With high gains, machines can cut more parts in an hour because the axes respond faster, and for the same reason, finishes are smoother because the servos reject disturbances better during the cuttin process.