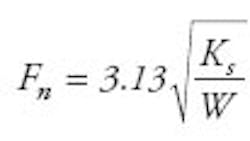Vibration Pacification
When you bring various complex mechanical and structural components together to form a functional motion system, modeling and predicting the resultant dynamics is usually difficult. Sometimes, the combination of drive components – gearbox, motor, belting, and so on – causes unacceptable noise or vibration, even though the parts operate smoothly and quietly alone. Besides being plain loud, the dynamic interactions may lead to inaccuracy in a servo system, or even a moderate sound signature that is objectionable in a given environment. Then there are cases where unchecked vibration induces high cyclical stresses and consequent mechanical failure.
By looking ahead early in the design process, these shaking problems can be forestalled. Low-cost, passive techniques and devices, properly applied, can usually suppress the effects of vibration through isolation or damping.
Isolating bad vibes
A common noise problem occurs when a stepper motor’s vibration is transmitted through the mounting structure and into an enclosure – a thin, rigid panel – and becomes amplified and broadcast as radiated sound.
In this instance, the most effective way to reduce vibration in the structure is by isolating its source. An isolation system, by definition, must allow relative motion between the vibration source and support structure. This is typically accomplished with some type of resilient connection between the two. Properly applied, the resilient interface will support static loads – due to or acting upon the source – while “filtering” the dynamic forces generated by the source. An improperly designed system, though, can amplify transmitted vibrations and make things worse. This phenomenon can be clarified by referring to a graph showing transmissibility characteristics of a basic, single-degree-of-freedom isolation system.
An isolation system’s effectiveness is typically measured in terms of transmissibility Tr – the ratio of acceleration transmitted into the mounting structure to the acceleration present in the source. When Tr > 1, the system amplifies vibration. When Tr < 1, the system provides isolation. All passive isolation systems exhibit these two distinct frequency regions of amplification and isolation. The objective when designing the system is to ensure the source’s problem frequency ends up far enough into the isolation region to achieve a high enough level of vibration reduction.
Peak transmissibility, the largest vibration amplification, occurs at the isolation system’s natural or resonance frequency Fn, which is determined by the weight of the isolation source W and the isolation system stiffness Ks:
The amount of damping in the isolation system will determine the magnitude of this peak transmissibility. As damping increases, the magnitude will decrease. For metallic spring-based mounting systems, peak transmissibility can reach 20 or 30. For lightly damped rubber systems, it can approach 10.
Certain highly damped proprietary elastomeric systems can have a peak transmissibility value as low as 1.5. Elastomer-mount damping is often described in terms of a material loss factor ηm which is equivalent to twice the critical damping ratio. Using mounts with a high level of hysteretic damping can minimize amplification at the resonant frequency. This is especially important when a system cycles from high to low speed during operation or generates impulse forces – keep in mind that stepper motors can deliver such “stepped” impulse forces, and therefore can excite an isolation system’s natural frequency.
The point where the amplification region meets the isolation region defines the system’s crossover frequency FCO which typically occurs at 1.414 Fn. Vibrations above FCO (into the isolation region) will be isolated – their transmission diminished – at a rate of about -12 dB per octave of frequency increase.
Proper mount selection, key to an effective isolation system, requires a basic understanding of motion system components – operational conditions and dimensional information – and access to the mount manufacturers’ performance data.
Here is a list of the primary items required to specify an isolation mount:
• Weight of motor or other vibration source
• Number of mounting points
• Problem frequency to be isolated from mounting structure
• Desired level of vibration reduction or transmissibility
• Miscellaneous information on mounting scheme and orientation of source, e.g., type of mounting hardware, attachment point dimensions, available space, mounting plane orientation, service temperature range.
Most commercial suppliers of isolation mounts supply stiffness data in their list of selection parameters. The items above will determine the maximum allowable isolator stiffness. Once this value is known, it can be compared to the listed catalog values. Maximum stiffness can be calculated with the following equation.
Tr = desired transmissibility (Tr = 1–[%isolation efficiency/100])
As an example, if a five-pound motor with four mounting points has a forcing frequency of 475 Hz, and you desire an isolation efficiency of 80%, the above equation yields a maximum mount stiffness of 4,798 lb/in. The next step is to scan the catalogs and find a mount of the right size and configuration, with a stiffness no greater than this calculated value. As for how far below maximum stiffness you want to go, softer mounts deflect more under dynamic and static loads, so it’s usually desirable to mount components more rigidly.
Once we know the mounting stiffness, we can check static deflection x by using Hooke’s Law, x = P/K, where P is any static force (including the source weight) and K is the system stiffness. For the above example, the static deflection from the motor weight is 0.001 in.
Isolation system design may necessitate other considerations, depending upon the situation. For example, in the case of mounting a computer hard disk drive in a desktop workstation, it is not only important to isolate higher-frequency spindle and actuator vibrations, but also to limit lower-frequency resonant deflections coming from the electromagnetic read-write head. Isolator damping can help minimize this resonant deflection while still allowing the flexible isolator to restrict the higher frequencies. Similar considerations will apply to a high-speed position-critical stepper motor mounting system.
As a last note, it is very important to provide a highly rigid mounting point for isolators. Since the mounting structure’s attachment points also exhibit flexibility, the interface region is actually behaving like two springs connected in series – one with the stiffness of the resilient material, the other with that of the structure. However, the system has been designed only around the isolator’s characteristics; therefore it is best if the isolation mounts carry at least 90% of the total deflection. As a rule of thumb, mounting points should exhibit 10 times the isolator’s stiffness.
Damping out structural resonance
Occasionally, it is impossible or impractical to incorporate an isolator into a motion system. This is usually because the vibration source (say, the motor) cannot be allowed any movement whatsoever relative to the mounting structure. When such situations arise, a structural damping treatment can often solve the problem.
Structural resonances are inherent in any system – mass and stiffness are all that’s required. Source vibrations often excite these resonances, and are thereby amplified and efficiently conducted from one component to another. A source that produces vibration in the frequency range of a system resonance will often be the dominant producer of troublesome vibrations. An effective damping system in the surrounding structure will dramatically reduce the resonant buildup of energy, thus reducing the amount of vibration transmitted to other system components and structures.
All materials exhibit some level of damping, described by a loss factor ηm. However, most structural materials have very little internal damping, and their resonant behavior makes them excellent radiators of noise and conductors of vibration. This applies to all solid metallic materials, which exhibit material loss factors from 0.0001 to 0.002, and most rigid structural plastics, with loss factors from 0.01 to 0.05. In contrast, damping materials exhibit loss factors well in excess of 1.0.
When designing a structural damping treatment, it is common to achieve a tenfold increase in system loss factor. This can mean a 20-dB reduction in resonant vibration and (estimated) “large panel” radiated noise (which assumes that the wavelength of the bending wave is small relative to panel dimensions). Actual noise reductions will vary depending on the proportion of this resonant noise to the overall system noise.
Another part of assessing a damping treatment’s effectiveness is to compare driven versus resonant vibration. Damping treatments rarely do much for forced, non-resonant vibration. Instead, such vibrations are best dealt with by the deliberate addition of mass or stiffness to a structure. (Since damping treatments do add some small amount of mass and dynamic stiffness, there are certain instances where they make a better-than-negligible difference with driven vibrations.)
Damping treatment typically consists of a viscoelastic polymer sheet with a high material loss factor. The sheet is applied onto a structural component. The two methods of passive structural damping are termed extensional and constrained- layer damping.
Extensional damping presents the most basic form of material application. The damping material is simply attached to the structure with a strong bonding agent. Alternatively, certain materials may be troweled onto the surface, or the structure may be dipped into a vat of liquefied material that hardens in a curing cycle. Once adhered, this damping layer dissipates vibration energy internally through tension and compression induced by the vibratory flexing of the structure.
The effectiveness of this method increases with damping layer thickness. Damping material properties – elastic modulus and material loss factor – will also influence damping performance. Also bear in mind that these materials’ damping properties vary with temperature.
Because calculations for system loss factor are complicated, the damping material manufacturer is the best source regarding the effect of a particular material and treatment thickness on a specific structure. Materials experts typically use a computer program to quickly calculate system loss factors and largepanel noise reduction values for a variety of material and thickness options.
Stiffer structures usually require constrained-layer damping. In this arrangement, the damping material is sandwiched between a structural constraining layer and the base structural layer. When such a system flexes during vibration, shear strain is induced in the damping material. Due to the damping material’s properties, a portion of the energy carried by the damping layer dissipates internally as low-grade heat. For constrained-layer damping treatments, the method of attaching the layers does not matter as long as adequate surface contact and coupling occurs; thus, the layers may be bolted, riveted, or glued. If adhesives are used they should possess high shear stiffness, as softer adhesives will not adequately transfer shear strain to the middle (damping) layer. As a general rule, if the constraining layer is the same material as the base structure, it should be half the base structure’s thickness.
Unlike extensional damping treatments, where a thicker treatment always means more damping, with constrained-layer systems a thinner damping layer often provides better results. As with extensional arrangements, the damping material manufacturer can provide the best insight on installation and buildup options for various damping and constraining layer materials and thicknesses.
System loss factors for constrained- layer damping are extremely cumbersome to calculate and require a specialized computer program along with comprehensive data on the materials’ dynamic properties. Therefore it is important to work with materials that are well defined in these properties. Because such information is not typically found in common material databases, it’s often necessary to work with manufacturers that specialize in damping materials.
With structural damping, placement of the treatment is very important. It’s usually impractical or impossible to cover 100% of a structure. But try to apply the damping treatment on all areas that undergo high flexural strain. Understanding where these areas are in complex structures often requires knowledge of mode shapes associated with troublesome frequencies. On simpler structures such areas can generally be determined by inspection.
Tuned dampers
For position-critical equipment driven by stepper motors, such as disk drives, printers, and robots, speed and accuracy define the performance. But some amount of inaccuracy or instability is inherent with such equipment. Because of inertia, “seek-and-stop” stepper motor functions are actually “seekand- settle.”
Unlike most electric motors, stepper motors rotate in finite steps, typically about 400 or 800 steps per revolution. When a stepper motor surges through the right number of steps and tries to stop, inertia causes the driven component to overshoot its target. Resonant oscillation continues until the drive settles or until the movements are small enough for the driven component to fulfill its function.
To optimize system performance in a stepper motor application, you need to minimize the magnitude and duration of these settling oscillations without impeding normal operation. Tuned dampers that incorporate highly damped viscoelastic elastomers can do the job costeffectively while reducing system instability problems.
A rotational tuned damper employs a ring-shaped mass that slides onto an elastomeric ring, which in turn attaches to the drive shaft. It is advisable to use an elastomer with high internal damping. Both the mass and the elastomer ring move with the rotor, but the mass’ inertia causes it to lag slightly. The small angular difference generates shear strain in the elastomer ring, thus producing the necessary damping.
A tuned damper’s effectiveness lies in the characteristics of the damping elastomer and the amount of added mass. The additional inertial mass is typically around 25% of the drive’s total rotational inertia (before the tuned damper system is attached). Drive inertia can be approximated by summing the mass moments of inertia of individual driven rotary components, including the motor shaft assembly.
Once the inertial mass is determined, the elastomer ring geometry must be calculated to provide the appropriate torsional stiffness. This parameter is adjusted to tune the coupled inertial mass resonance, which should be midway between the system resonance with the inertial mass installed and locked in place, and the resonance without it. This tuning process can be somewhat iterative and require several rounds of prototyping. More information on tuned inertial dampers can be found in Shock and Vibration Handbook, edited by Cyril M. Harris.