One thing engineers learn very quickly about position control systems is that they are inherently unstable. Consider a typical closed-loop system, consisting of a motor, current amplifier, and position sensor.
Suppose the motor starts at 10° and is required to stop at 0°. Since the motor is out of position, the system generates a current proportional to the error. The current, in turn, energizes the windings, producing a torque that accelerates the shaft toward 0°.
As the motor approaches zero, the position error decreases as does acceleration. Velocity, however, continues to increase — so by the time the motor reaches its intended destination, it’s going too fast to stop and is likely to overshoot the position by as much as 10°. This sets up the reverse process, causing the motor to go back and forth indefinitely. Obviously, some sort of compensation is needed to stabilize the system.
To better understand compensation, consider the similarity between a position control system and a pendulum. Both behave according to the same dynamic equations, evidenced by the same sort of sinusoidal motion.
In the case of the pendulum, if you want to stop it from oscillating, you can submerge it in oil. Actually, any fluid with viscous damping properties – where resistance is proportional to velocity – will work. A similar opposing force, if proportional to rotor velocity, can be applied to a motor to stabilize a positioning system.
Since motor position is known, a differentiator is all that’s needed to find velocity. Now when the control loop is closed, two operations are performed: The first creates a corrective signal proportional to the error. Its dynamic effect is like that of the force of gravity on the pendulum. The second operation, based on the derivative, has an effect analogous to viscous damping. Working together, the two operations cause the motor to move, like a damped pendulum, to the desired position in a stable manner. The proportional and derivative terms give this control technique its name, PD compensation.
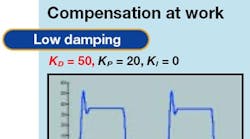
Stability is only half the problem, however. Consider a system with PD compensation trying to stop at 0°. Suppose the motor stops close to but not exactly at zero. The resulting torque produced by the small position error may not be sufficient to overcome friction and move the motor the rest of the way. The range of positions where the motor may stop short of its destination is called the deadband, and is a reflection of system accuracy.
To correct such position errors, an integrator may be added to the compensation algorithm. With an integrator, the drive signal continues to increase as long as there is a position error. Thus, even a small error will eventually result in a corrective action. It may take 20 msec or so, but with PID compensation, positioning systems are guaranteed to be more accurate than those without it.
Dr. Jacob Tal is president and cofounder of Galil Motion Control Inc., Mountain View, Calif. He can be reached at (800) 377-6329 or [email protected].