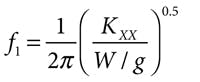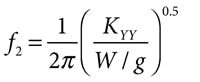Preventing oil whirl for better bearing operation
Oil-whirl instability in rotor bearings was discovered by General Electric engineer Burt Newkirk in the 1920s. Since then, much has been written about design methods to reduce its harmful effects. Yet it still remains troublesome and of great concern, particularly in lightly loaded journal bearings in turbines, compressors, and pumps; in large vertical motors and generators; and in many similar machines.
Here’s a brief review of the physical nature of oil whirl, some ways to reduce or eliminate its effects, and alternative designs to avoid it altogether.
Vibration basics
Three types of shaft vibration are particularly pertinent to fluid-film journal bearings:
Unbalance vibration is almost always caused by a lack of balance in the rotating mass supported by the bearings. This type of vibration can be alleviated or eliminated by carefully balancing the rotor.
Half-frequency oil whirl, a type of rotary-shaft motion, is caused by a wedge of oil film traveling around the bearing circumference at an average velocity of half the shaft’s surface speed. Amplitude of this rotor whirl often approaches 50 to 100% of the total clearance and threatens machine performance.
Oil whip, a potentially catastrophic vibration, occurs when whirl frequency coincides with the natural frequency of the shaft at rotational speeds two or more times the rotor’s natural frequency. This might be thought of as a stabilized version of half-frequency whirl. Its constant frequency is half the first natural frequency of the shaft for speeds ranging up to about three times the natural rotor frequency.
The effects of these three conditions are shown graphically in Rotor-vibration frequency.
Complexities associated with the oil film, bearing geometry, temperature, viscosity, supporting structure, and the like make it difficult to predict rotor instability. In fact, different machines may respond differently with the same bearings, and secondary effects may influence the type of vibration.
For example, as speed increases unbalance may delay a shift from simple rotational frequency to expected half-frequency oil whirl. On the other hand, at speeds up to around three times the natural rotor frequency, unbalance vibration takes over and amplitude rises to the maximum possible within the bearing clearance.
Nature of oil whirl
What causes whirl? The answer involves the interaction of external forces on the bearing and internal oil-film pressure generated within the bearing clearance.
Ideally, entrained oil in the bearing clearance circulates with an average velocity of about half the shaft surface speed. But in practice, it is between 40 and 48% of shaft speed. With a load on the bearing, the shaft center becomes eccentric and the shaft surface rides on the crest of an oil film.
Now, with normal radial displacement of the shaft, oil pressure on the upside of the close clearance zone will be higher than on the downside. The resulting tangential force in the direction of rotation tends to induce “forward whirl” of the journal. With this whirl, the increasing tangential force reduces the clearance further to produce an increasingly higher destabilizing tangential force. Field experience has shown this whirl frequency is typically less than 2% below half the rotor speed.
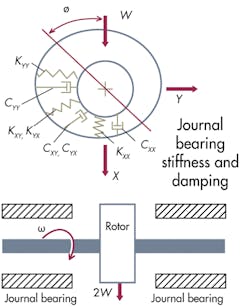
Let’s look at some highly simplified features of oil whirl. The graphic, Journal bearing stiffness and damping, represents an idealized rotor of weight 2W supported on two identical bearings. The load on each bearing is W, and the bearing center is displaced to a steady operating position as shown. One can draw a line connecting the shaft and bearing centers, and the load line, to form an attitude angle ø. It’s unique to the bearing and operating condition.
In general, the lowest natural frequency is No = ωo/2π, where ωo = (k/m)0.5 with k representing shaft stiffness and m the rotor mass. While the equivalent spring constant for vertical displacement is not linear over any extended range, a value KXX can be taken as the differential displacement in the vertical direction (X) with a differential change in W (as with a rotor imbalance or varying external force). With no rotor flexibility and negligible damping, the bearing vertical natural frequency becomes, as for any simple spring-mass system:
The first subscript of KXX indicates that the weight, W, produces a force in the X direction; the second subscript indicates that this K is for motion in the X direction. KXY is the spring constant related to displacement in the oil film in the Y direction under a force in the X direction.
Because a softer spring constant KYY is encountered in the unloaded horizontal direction, the bearing horizontal natural frequency becomes:
Similarly, one can define damping coefficients CXX and CYY in the vertical and horizontal directions. For other than pivoted-pad bearings, cross-coupling coefficients must also be introduced (KXY, for instance) as a spring constant for motion in the Y direction, for varying vertical load W in the X direction. Forces induced by the cross-coupling coefficients tend to drive the rotor into an orbit. Typically for light loads in fixed-arc bearings with cross-coupling, this orbit frequency is close to half the journal rotational speed.
If damping and load are not sufficient to suppress this cross-coupling force, the rotor may break violently into an uncontrolled whirl orbit, or rotor whip, with an amplitude closely matching the full internal clearance in the bearing.
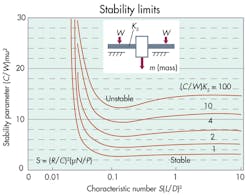
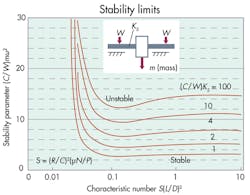
Stability characteristics of a rotor carried on a full 360° journal bearing can be estimated from the Stability limits graph. These results are based on the so-called short bearing approximation valid for bearings with L/D ≤ 1 and apply only for laminar flows.
Greater shaft flexibility (lower Ks) tends to decrease stability. Kscan be approximated from simple beam theory by dividing the rotor weight by the midspan deflection resulting from that weight. (A more-detailed analytical background and oil-film response coefficients for fixed-arc and pivoted-pad bearings are provided by “Journal and Thrust Bearings” by A. Raimondi and A.Z. Szeri; and “Fluid Film Lubrication” by H.J. Sneck and J.H. Vohr. Both can be found in the CRC Handbook of Lubrication, Vol. II, CRC Press, Boca Raton, Fla., 1984.) More-recent computer routines using numerical solutions deal with the effect of temperature on the bearing’s dynamic behavior.
Stability example
Here’s an example of how to predict behavior. Determine whirl stability for a 5,000-lb horizontal rotor in its cylindrical bearings with the following characteristics: diameter D = 2R = 6 in.; length L = 3 in.; radial clearance C = 0.006 in.;
N = 60 rev/sec (3,600 rpm); lubricant viscosity µ = 2 ×
10-6 lb-sec/in.2 (reyns); and rotor stiffness Ks= 10 × 106 lb/in.
Load or rotor mass m = W/g = 5,000/386 =13.0 lb-sec2/in.
Unit load P = W/(DL)= (5,000/2)/(6 × 3) = 139 psi.
Sommerfeld number S = (R/C)2 (μN/P) = (3/0.006)2 (2 × 10-6 × 60/139) = 0.216.
Bearing characteristic number S(L/D)2 = 0.216(3/6)2 = 0.054.
(C/W)Ks = (0.006/2,500) × (10 × 106) = 24; and
(C/W)mω2 = (0.006/2,500) × 13.0 × (2π × 60)2 = 4.43.
Referring to the Stability limits graph, because the coordinate point S(L/D)2 = 0.054, (C/W)mω2 = 4.43 lies below the curve for (C/W)Ks = 10 and the rotor will be free of oil-whirl instability.
If the speed were raised to 7,200 rpm, however, repeating the above calculations shows that S(L/D)2 = 0.108 and
(C/W)mω2 = 17.72, which falls in the unstable region.
If the bearing is unstable, ways to a shift to the stable operating region include:
- Increasing the unit bearing load, commonly above 80 to 100 psi in industrial turbines, compressors, and similar units.
- Shortening the bearing length L.
- Varying the bearing internal clearance, viscosity, or some other combination of pertinent factors to shift operation into the “stable” zone of the stability curve.
While the above example and the Stability limits graph provide guidelines for relating factors that influence the onset of oil whirl, the complexity of rotor-bearing systems has led to some uncertainty in field observations about the interacting effects of oil viscosity, shaft alignment, and other related parameters.
Whirl-instability problems are typically associated with common sleeve bearings with cylindrical bores. This type is widely used in industrial machines because it is simple to design, inexpensive to manufacture, and provides maximum load capacity.
If one encounters whirl in an existing machine, simply cutting a circumferential groove at the bearing midlength will often provide stability with no need for any related bearing changes. This central groove effectively divides the bearing into two short bearings and cuts the minimum oil-film thickness by some 15 to 20%. It has the same effect as increasing the total load on the original full-length bearing. Using three or four axial oil-feed grooves, instead of the usual two, will also lower load capacity for somewhat better whirl prevention.
Engineers should also consider using one of the more-stable journal bearing types to overcome instability, or prevent it in designs where oil whirl is a concern.
An elliptical bearing is commonly used in industrial and electric-utility turbines and generators. The loaded lower half of the bearing gives an equivalently lower R/C ratio, and some additional stabilizing pressure is generated in the wedge-shaped clearance for the oil film entering the top half.
A three or four-lobe bearing can potentially offer some centering action on the journal as it passes each segment to deter whirl.
With centering forces at each pad and no cross-coupling response coefficients, the tilting-pad design is essentially free of oil whirl. Higher cost, higher power loss, and complexity in machining and assembly, however, commonly mean this design is only used in the most demanding high-speed machines.
Edited by Kenneth J. Korane