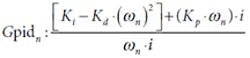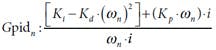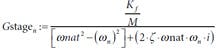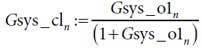Cloud-based graphical tools simplify motion design
Many positioning stages used in process applications — such as semiconductor manufacturing, microelectronic assembly, lab automation, and light machining — are characterized by attributes such as light inertial loads, short travel, small footprints, and low cost. But these same tasks may demand high throughput, high jerk, high acceleration, high velocity, high precision, and smoothness of motion, all with high reliability.
It can be tough to design a motion system that meets both sets of constants. The challenge lies in optimizing the system while keeping costs down. System analysis tools such as Mathcad and Matlab may help by modeling performance as a function of various system parameters and operating conditions.
But, by turning to the Internet cloud, it’s possible to develop a simplified graphical tool resembling Mathcad and Matlab in concept that engineers can use interactively to quickly analyze various positioning stage configurations.
The tool can quickly estimate answers to questions such as:
What is the settling time of a Parker LCR30 ball-screw stage and LCR30 belt-driven stage, on a 3-mm move, with 3-kg load, to an accuracy of 150 •m?
Getting such answers with tools like Matlab may require expert modeling and costly, licensed software. It may be time consuming and expensive to test individual stages. On the other hand, cloud-based tools may give good estimates within a few minutes of trial-and-error runs.
Such tools have several advantages. First, in many cases the tool is free to use on the Web. Second, operation is usually self-explanatory with 24/7 availability in the cloud. Third, the tool is usually accessible by PC, cell phone, or even tablet. Combined with a manufacturer’s database of related components, the tool can help choose the optimum product for an application.
Model description
At Parker, we model our positioning-system analysis tool as a closed loop. It consists of two blocks, one for the controller/amplifier and another for the stage that includes motor, actuator, and a moving load. The operation and interaction of these block is defined by the controller transfer function:
the stage transfer function:
the open-loop transfer function:
and the closed-loop transfer function:
where ωnat = natural frequency, ζ = damping coefficient, and n = sample point. The four equations simulate the time response of the stage with a Runge Kutta fourth-order numerical integration.
For the frequency-response analysis, the gain and the phase angles in the equations are:
where G = gain, R = real component of the complex transfer function in the four equations, I = imaginary component of the complex transfer functions, and Ph = phase.
System parameters
The stage is characterized by its moving mass, stiffness, structural damping coefficient, and motor constant. The controller is characterized by its proportional, derivative, and integral gain settings and the step function setpoint.
These parameters may be changed interactively by trialand- error iterations to either represent known system parameters of potential stages or as trial parameters. Trial parameters may help reach and confirm desirable system characteristics or a desirable performance variable.
Operation of the application is controlled by a set of operating buttons. Once the system parameters are entered, either manually or by clicking the Example button, a click on the Run button lets the engineer observe the results. A Clear button erases the input variables permitting a new start from scratch.
System variables
The application output first shows the output variables that the tool generates, including stage characteristics and controller-filter characteristics. Stage-characteristic variables include natural frequency and structural-damping coefficient. The controller-filter characteristics include a corner frequency for the integral gain and a corner frequency for the derivative gain.
Note that once the moving weight is known, the damping coefficient and the stiffness may be estimated to generate the desired stage characteristics by iteration. Here are the typical stage characteristics derived from the working example:
The choice of PID variables automatically determines the corner frequencies of the controller. The corner frequencies assist the tuning process in selecting the PID gains for the desired stage performance.
System performance in the time domain
With the response plotted in the time domain, the graph shows the position response of the stage to a step input. It should be noted that the user needs to indicate the time interval for the step response and the settling window for which settling time will be calculated in the yellow boxes. The results in the blue boxes include the maximum amplifier current required to make this move, along with the maximum power that the motor needs to generate. The results also indicate the maximum values of the jerk, acceleration, and velocity of the stage. Finally, the results show the settling time to the desired precision window.
Settling time is an important variable of positioning systems. Many positioning applications, such as auto focus in scanning microscopes, may operate in repetitive small steps many thousands of times an hour. This requirement means that throughput critically depends on settling time and that optimum performance demands a minimal settling time. The tool lets the user quickly try out various stage configurations, with various controller parameters, in an attempt to optimize the desired move. Users can optimize for minimum settling time subject to constraints such as maximum current, maximum acceleration, maximum velocity, or maximum jerk.
Plant-frequency response
The plant-frequency response is a quick graphical means of presenting the stage characteristics. As shown in the gain chart, the corner frequency is close to 10 Hz. The exact value is 13 Hz. The structural damping is high as indicated by the low amplification. Up to the corner frequency the gain — which is the ratio of the current amplitude and the output position amplitude — is relatively constant. For frequencies higher than the corner frequency, the gain drops at a rate of 40 dB per decade. The phase, as expected for a second-order system, starts at 0° in low frequencies, passes through –90° at the corner frequency and ends up at –180° at high frequencies.
PID tuning may not be an easy task. However, it is critical to optimize system performance. Although the literature is saturated with examples of PID analysis, it is quite difficult for a nonservo expert to follow its principles in a relatively short time. It should be noted that most modern servocontrollers have one form or another of PID filters. And many widely used controllers, such as the Parker ACR, include additional filters such as feed-forward observers and notch filters, which are outside the scope of this article.
The first observation is that the PID gain has a trough shape. The bottom is determined by the proportional gain. For example, a proportional gain of 10,000 sets the bottom of the Gain graph at 80 dB. Recalling that the definition of a dB = 20 × log of the gain, it implies that dB = 20 × Log 10,000, which is equal to 20 × 4 or 80 dB.
The next observation is that the left side of the trough is a low-pass filter which boosts the gain of low-frequency inputs. This result is from the integrator gain. The integrator operates over a long period; therefore, the lower the input frequency the longer the time before position change takes place and, therefore, the higher the gain. It should also be noted that the integral gain drops at a rate of 20 dB/decade, crossing the bottom of the trough, as set by the proportional gain, at the corner frequency around 10ˆHz. The exact value in the example is 19 Hz.
Similarly, the right side of the trough is the derivative gain. It is in fact a high pass filter, which amplifies the high frequency gains. Intuitively, the higher the frequency the higher the rate-of-change of position and, therefore, the resulting derivative gain is higher. Notice that the integral gain ramps up at a rate of 20 dB per decade. The corner frequency of the derivative gain is around 100 Hz. Once again, the exact value of the derivative corner frequency is 31.8 Hz.
A closer look at the phase chart reveals that it starts at –90°and gradually increases to 90°. Between these two limits, the phase chart goes through –45° at the integral corner frequency. It then continues through 0°, at the center of the proportional gain region, and through 45° at the derivative corner frequency.
We may use these corner frequencies of the integral and derivative gains and the bottom trough of the proportional gain as cornerstones to shape up the PID frequency response and reach the desired performance.
Open-loop transfer function
The open-loop gain is the sum of the plant gain and the controller gain. Similarly, the open-loop phase chart is the algebraic sum of the plant phase and the controller phase.
The important system performance variables drawn from the open-loop diagram are the position bandwidth and the stability margins. The position bandwidth is the cross over frequency at which the gain crosses the –3 dB line. In the example it’s about 20 Hz. The stability of the system is measured by the phase margin and gain margin. The phase margin is estimated to be 40°, the difference between the phase at the crossover frequency (–140°) and the -180° point. The preferred practice is a minimum phase margin of 45° for a robust design. Robust servosystems are defined as systems that display minimal sensitivity to changes in parameters.
The gain margin is another stability variable determined from the open loop diagram as the distance between the gain at –180° phase and the 0-dB line. In the example it is not relevant because the phase diagram does not cross the –180° line.
In summary, the objective of PID controller tuning is to shape the open-loop diagram to maximize the position bandwidth while maintaining good stability margins. Different stage types produce differing position bandwidths with times to settle within a 1-Œm position.
Closed-loop transfer function
The closed-loop frequency response of the system shows the gain for lower frequencies is close to zero up to the corner frequency. Then it gradually changes its form and starts resembling the shape of the open-loop chart at higher frequencies.
Similarly, at lower frequencies the phase is close to zero and, as the frequency rises beyond the corner frequency, it starts to resemble the shape of the openloop chart.
The following is an example of a positioning stage for semiconductor metrology application.
The positioning specification is for a stage moving a load of 15 kg, a step size of 2 mm and settling to 0.05 Œm in less than 140 msec with an amplifier current that does not exceed 15 A. The simulation ran as shown using the tool at optineer.com/Analysis.
Within 10 min, trial-and-error testing determined the least-expensive motor that will do the job. It has a force constant of 54 N/A, equivalent to the Parker Trilogy 310-4. The simulation assumes ~92-Hz natural frequency for the stage with a typical linear motor structural damping of ~0.03. The resulting maximum current was ~12.5 A and the move and settle of a 2-mm step to 50 nm completed in 81.2 msec. The simulation also shows the PID gains used to get this performance. The results indicate a bandwidth around 15 Hz.
As demonstrated, simple analytic tools may reside on an internet cloud server and be available for users 24/7 as free promotional support. It should be made clear, however, that such tools depend on the assumptions used. Therefore, these tools, such as the one presented in this article, must be used with caution and their results should always be validated by other tools or actual testing.
Edited by Robert Repas. For more information, visit the Parker Hannifin Daedal Div. website.