Determining the service or useful life of screw actuators – lead (acme), ball, and roller screws is a fundamental problem that faces many motion-system designers. In a broad sense, a screw’s service life defines how long it will operate and satisfy its required function. Designers and engineers must consider several factors when calculating realistic expectations of screw life. These factors include fatigue, corrosion, load-life relationships, excessive wear, contamination, insufficient strength, and dynamic and static loading.
Here’s a closer look at the roles these factors play, and how to properly determine the life of screw actuators. This information will let design teams make “apples-to-apples” comparisons of motion-control components. Also, examples of load-life conversion calculations will demonstrate the importance of load on screw life and how application requirements sometimes need to be modified to lengthen an actuator’s life.
Fatigue failures
A ball or roller screw actuator’s fatigue life is influenced by its internal design, the materials it is made of, and how it’s manufactured and lubricated, as well as operational conditions such as load, velocity, and temperature. The steel used in screw assemblies these days is practically free of impurities, and is of high quality. However, inevitable imperfections and non-metallic inclusions in the steel lead to fatigue failures that will eventually end every ball and roller screw’s service life.
Fatigue life is most heavily influenced by the applied load, and fatigue failures are caused by cyclic compressive stresses between balls or rollers and threads. Rolling components support applied loads, which creates high stresses beneath the thread surfaces. Gradually, this leads to in-groove flaking (metal on the surface of the screw falls apart in the form of scales).
Predictability of life
Predicting lead-screw life under laboratory conditions differs for various screw types.
Recirculating ball screws and planetary roller screws, however, are similar to ball or roller bearings in that they all behave as rolling-contact devices. As a result, engineers can apply life evaluation standards and methods developed over the years by the American Bearing Manufacturers Assoc. for radial ball and roller bearings. The concept of life fatigue, or basic rating life, was first defined for radial bearings and later extended to ball and roller screws.
By contrast, acme lead screws are sliding-contact devices. Wear rates of the nut material, usually plastic or bronze, are generally nonlinear, making it difficult to predict life even under controlled conditions. One of the critical life factors for “solid” nuts is heat buildup in the nut due to sliding friction. The velocity of motion and weight of the load the nut moves also help determine its life. Because the lifespans of acme lead screws depend on so many factors, those lifespans vary considerably. That’s why most manufacturers do not provide life data for these products. Life estimations for machines and components equipped with acme screws typically have to be based on empirical data such as test results and experience.
International Standard ISO-3408-1 defines ball screw life as “the number of revolutions the ball screw shaft makes in relation to the ball nut body before the first evidence of fatigue develops in the material of screw shaft, nut body or in the balls or rollers.” Another term, basic rating life, known by the symbol L10, is used for individual ball screws or groups of apparently identical ball screws operating under the same conditions. It is the length of time the screw(s) have a 90% probability successfully reaching.SH: Load-life relationship
Standard engineering practices suggest that life estimation of any machine containing a ball or roller screw must be based on the screw’s L10 life. Basic dynamic axial load rating, C, is a constant load acting axially and centrally on a ball or roller screw that results in the screw operating for a basic L10 rating life equal to one million revolutions.
This file type includes high resolution graphics and schematics when applicable.
Dynamic load rating, (measured in N or lbf) is provided by ball and roller screw manufacturers for all screw and nut combinations they offer. The magnitude of the dynamic load rating typically depends on screw pitch diameter, screw pitch (or lead), and the number and size of recirculating rolling elements (balls or rollers) inside the nut that simultaneously carry the load. Again, citing the ISO-3408-1 standards, the theoretical fatigue life of ball or roller screws is inversely proportional to the third power of the dynamically applied load.
If a load of the magnitude P needs to be applied to a lead screw, then a simple form of its load-life equation is:
L10 = (C/P)3 x 1,000,000 revolutions
where L10 is basic rating life; C is the dynamic load rating; and P is the application load.
This equation reflects a fundamental relationship between load and life, in which reducing the load on any given screw by half lengthens the life of the screw by a factor of eight. Inversely, increasing the load by 50% reduces life expectation to about 30% of its previous lifespan.
It is important to note that some screw manufacturers define basic rating life using units of measurement other than revolutions, such as inches, feet, or kilometers of travel. When comparing different products, engineers must convert dynamic ratings for all products they are considered to reflect the same L10 life parameters.
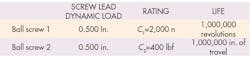
In one example of such conversion and comparison, a designer needs to compare the two ball screws shown in the table below.
First, convert the life of the second screw to revolutions (by dividing it by screw lead):
L10(2) = 1,000,000/0.500
L10(2)= 2,000,000 revolutions
Second, convert the dynamic load rating of the second screw to newtons:
C2 = 400 lbf x 4.45
C2= 1,780 N
Third, calculate the load rating of the second screw so life is reflected in 1,000,000
revolutions:
C2 = 1,780 N x (2,000,000/1,000,000)1/3
C2 = 2,243 N
The results show the load rating of the first screw is lower than that of the second one.
Let us assume that the first ball screw has been selected for an application. Then, consider the following application scenarios each with different objectives.
Scenario 1. The application’s load requirement is 500 N. What fatigue life can be
expected?
Expected fatigue life is calculated as:
L10 = (2,000/500)3 x 1,000,000 = 64,000,000 revolutions.
This is an illustration of the fact that lighter loads significantly increase life.
Scenario 2. The same screw needs to be loaded with 5,000 N. Can the load rating be exceeded and what are the consequences with regard to life?
Expected fatigue life is calculated as:
L10 = (2,000/5,000)3 x 1,000,000 = 64,000 revolutions.
Expected life is significantly lower than the basic rating life of 1,000,000 revolutions. This Illustrates that any screw can be overloaded at the expense of life.
Scenario 3. A screw needs a fatigue life of 100,000,000 revolutions. How much load can the screw carry?
Load that can be attained can be calculated as:
C = 2,000 x (1,000,000/100,000,000)1/3 = 431 N.
This shows that in order for the screw to last longer, its load should be decreased.
The above examples illustrate the L10 life-load relationship for rolling contact power screws.
Dynamic load factor
Fatigue isn’t the only factor defining the useful life of a lead screw. The screw is also affected by wear, corrosion, contamination, strength of screw ends, and nut attachments. Screws can also be subjected to a variety of dynamic elements inherent in the application such as load misalignment, and vibrations. Therefore, it is practical for a designer to apply some safety ratio when calculating screw life values.
Typically such safety ratio is provided by a dynamic load factor or coefficient, f = 1.5-2.0, included in the denominator of the load-life formula:
L10 = (C / P x f)3, x 1,000,000 revolutions
where L10 is the basic rating life; C is the dynamic load rating; P is the application load; and f is dynamic load factor.
SH:Varying load
When the load varies during the working cycle, it is necessary to calculate the equivalent dynamic load, Pe, acting on the screw axially and centrally, which if applied would have the same effect on screw life as the combined actual loads.
The equivalent dynamic load is given by the following equation:
Pe = ( (1/L) x (P13L1 + P23L2+ … + Pn3Ln)1/3
where Pe is equivalent dynamic load; P1, P2, ... , Pn are varying loads; L1, L2, ... , Ln are the distances associated with varying loads, respectively; and L is the total distance traveled.
For example, consider an application with a total stroke of 12 in. and a load of 30 lbf acting over the first 8 in. of travel and 100 lbf acting over the remaining 4 in. of travel. The equivalent dynamic load for this application’s life evaluation can be calculated as:
Pe = ((P13L1 + P23 L2+ … + Pn3Ln)/L)1/3 or,
Pe = ((303 x 8 + 1003 x 4) /12)1/3 = 70.6 lbf
where L is 12 in.; P1 is 30lbf; L1 is 8 in.; P2 is 100 lbf; and L2 is 4 in.
Static load rating
Another screw characteristic provided by manufacturers is the basic static load rating. Although it does not affect life directly, it should be carefully considered when selecting ball or roller screws. The standard defines a basic static axial load rating of a ball screw, Co, as the static load acting axially and centrally, that corresponds to a total permanent deformation of ball and ball track at the most heavily stressed point of contact between the ball and the ball track of 0.0001 times ball diameter.
The fatigue life of screw actuators is heavily influenced by the load applied to the rolling components. Life can also be affected by wear, corrosion, contamination, and other dynamic elements such as misalignment and vibrations. Designers can predict the life of these components by applying load/life equations to specified screws, applying proper safety ratios, analyzing the results, and comparing the resulting performance after making all of the unit conversions. Engineers can get actuators with the proper life by carefully considering and calculating L10 values.