Forward progress
PID velocity control, as discussed in PT Design, March 1999, is quite common in analog motor drives. It's simple to implement and generally provides good performance. However, the iterative nature of PID loop tuning makes analog motor drives somewhat unwieldy on the factory floor. Digital systems, on the other hand, often use PI (proportionalintegral) velocity control, eliminating the derivative (D) term. PI loops are much easier to tune: First adjust P, then I, and you're done. PI control is ideal for applications that demand maximum responsiveness such as pick-and-place machines. On the down side, it doesn't cope well with low-frequency disturbances.
Low-frequency disturbances come in many varieties. Friction is on example, gravity is another. A control system that can maintain commanded velocity despite disturbances is said to be "stiff."
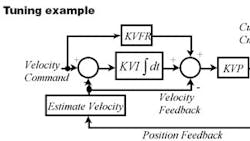
In integrating velocity controllers, low-frequency stiffness comes from the integral gain term. The problem with PI control is that this gain must remain relatively small to avoid excessive overshoot. To get around this dilemma, many engineers use feed-forward velocity control, or PDFF.
Like a PI controller, PDFF has an integral gainKVIand a proportional gain KVP. It also has additional feed-forward gain KVFR that independently controls the integral response of the system. By adjusting this gain, users can compensate for the normally small KVI term.
Suppose an application requires maximum responsiveness. Here, you don't need much integral gain, so you would set the feed-forward term KVFR high. (When KVFR is 100%, PDFF is identical to PI.)
Now consider an application on the other end of the spectrum, one that requires maximum lowfrequency stiffness. Here, you would set KVFR low, permitting a large integral gain without inducing overshoot. Don't forget that you're giving something up, however, namely responsiveness.
The majority of motion-control applications are somewhere in between these two extremes, such that a KVFR of about 65% provides generally good results.
Tuning practice
If you want to learn more about feed-forward control, like how to tune a PDFF loop, and download your free copy of ModelQ, a stand-alone simulation package.
After installation, click "Run" at top left, and select the April model from the combo-box (top center). Select the "Constants" tab and start adjusting the gains.
After you have entered a set of constants with a good step response, run a Bode plot (press "Go" near center-bottom) and check the bandwidth. Try tuning KVI with different values of KVFR. Note that increasing KVFR causes overshoot which can be removed by reducing KVI. Draw more Bode plots and watch the bandwidth go up as you increase KVFR. If you want to see the effect on responsiveness, look at the settling time associated with a step input. As the bandwidth goes up, the settling time goes down.
While you're working with ModelQ, here's a method you can use for tuning PDFF loops:
1. Tune KVP
• Command a step velocity.
• Temporarily configure PDFF as a proportional-only controller by setting KVFR = 100% and KVI = 0.
• Raise KVP as high as possible without causing overshoot or oscillation.
2. Set KVFR
• 100% for applications requiring maximum response
• 65% for general applications
• 0% for applications requiring maximum low-frequency stiffness
3. Tune KVI
• Raise the integral gain until you get 5% overshoot.
You can use this same procedure for PI control, skipping step 2. Remember, PI is just a special case of PDFF, where KVFR = 100%, and it works well in applications where lowfrequency stiffness is not critical.
As the worm turns
If you're using a motor to drive a worm gear, you'll probably want to tune your controller for maximum low-frequency stiffness (high integral gain) to overcome
friction. Otherwise, your system will tend to slow down at the end of each move as it attempts to pull into position. There's a catch here, though, because high integral gain is likely to produce intolerable settling times.
This is where PDFF controllers are ideal. With KVFR set to zero, you can safely increase KVI without the usual penalties. With PDFF, integral gains can be from eight to ten times higher than those associated with PI control.