Researchers Develop Way to Reduce Noise in Quantum Computing Hardware
Argonne researchers have reported a new method for reducing the effects of “noise” in quantum information devices, a challenge facing scientists around the globe working to meet in the race toward a new era of quantum computing.
Many current quantum information applications, such as carrying out an algorithm on a quantum computer, suffer from “decoherence,” a loss of information due to this noise. Decoherence is inherent to quantum hardware. Argonne researchers Matthew Otten and Stephen Gray have developed a technique that pulls the information out of the noise by repeating the quantum process or experiment many times in sequence or parallel with slightly different noise characteristics, and then analyzing the results.
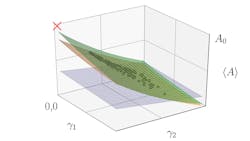
After gathering results from all the runs, researchers can build a hypersurface in which one axis represents the result of a measurement and the other two (or more) axes represent different noise parameters. The hypersurface lets researchers estimate the noise-free result and gives information about the noise.
This is a “hypersurface” fit to many experiments with slightly different noise parameters, ɣ1 and ɣ2. Black points are measurements of an observable with different noise rates. The red “X” is the noise-free result. Blue, orange, and green surfaces are first-, third-, and fourth-order fits. (Image: Argonne National Laboratory)
“It’s like taking a series of flawed photographs,” says Otten. “Each photo has a flaw, but in a different place in the picture. When we compile all the clear pieces from the flawed photos, we get one clear picture.”
Applying this technique effectively reduces quantum noise without using additional quantum hardware.
“You could create several small quantum computers and run them in parallel,” says Gray. “The results would also help extend the usefulness of the quantum computers before decoherence sets in.”
“We successfully performed a simple demonstration of our method on the Rigetti 8Q-Agave quantum computer,” says Otten. “This class of methods will likely see much use in near-term quantum computers.”
Otten and Gray have developed a similar and somewhat less computationally complex process to remove noise from results based on correcting one qubit at a time to approximate the result for all qubits being simultaneously corrected. (A qubit, or quantum bit, is the equivalent in quantum computing to the binary digit or bit used in classical computing.)
“In this approach, we assume the noise can be reduced on each qubit individually, which, while experimentally challenging, leads to a much simpler data processing problem and yields an estimate of the noise-free result,” notes Otten.