Latest from What's the Difference Between...
What’s the Difference Between Conduction, Convection, and Radiation?
Download this article in PDF format
Heat transfer is the physical act of thermal energy being exchanged between two systems by dissipating heat. Temperature and the flow of heat are the basic principles of heat transfer. The amount of thermal energy available is determined by the temperature, and the heat flow represents movement of thermal energy.
On a microscopic scale, the kinetic energy of molecules is the direct relation to thermal energy. As temperature rises, the molecules increase in thermal agitation manifested in linear motion and vibration. Regions that contain higher kinetic energy transfer the energy to regions with lower kinetic energy. Simply put, heat transfer can be grouped into three broad categories: conduction, convection, and radiation.
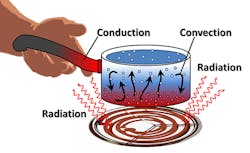
The image above, provided by NASA, highlights how all three heat-transfer methods (conduction, convection, and radiation) work in the same environment.
What is Conduction?
Conduction transfers heat via direct molecular collision. An area of greater kinetic energy will transfer thermal energy to an area with lower kinetic energy. Higher-speed particles will collide with slower speed particles. The slower-speed particles will increase in kinetic energy as a result. Conduction is the most common form of heat transfer and occurs via physical contact. Examples would be to place your hand against a window or place metal into an open flame.
The process of heat conduction depends on the following factors: temperature gradient, cross-section of the material, length of the travel path, and physical material properties. The temperature gradient is the physical quantity that describes the direction and rate of heat travel. Temperature flow will always occur from hottest to coldest or, as stated before, higher to lower kinetic energy. Once there’s thermal equilibrium between the two temperature differences, the thermal transfer stops.
Cross-section and path of travel both play an important part in conduction. The greater the size and length of an object, the more energy that’s required to heat it. And the greater the surface area that’s exposed, the more heat is lost. Smaller objects with small cross-sections have minimal heat loss.
Physical properties determine which materials transfer heat better than others. Specifically, the thermal conductivity coefficient dictates that a metal material will conduct heat better than cloth when it comes to conduction. The following equation calculates the rate of conduction:
Q = [k · A · (Thot – Tcold)]/d
where Q = heat transferred per unit time; k = thermal conductivity of the barrier; A = heat-transfer area; Thot = temperature of the hot region; Tcold = temperature of the cold region; and d = thickness of the barrier.
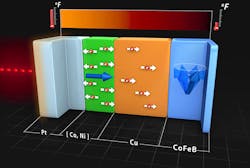
A modern of use of conduction is being developed by Dr. Gyung-Min Choi at the University of Illinois. Dr. Choi uses spin current to generate spin transfer torque. Spin transfer torque is the transfer of the spin angular momentum generated by the conduction electrons to the magnetization of a ferromagnet. Instead of using magnetic fields, this allows the manipulation of nanomagnets with spin currents. (Courtesy of Alex Jerez, Imaging Technology Group, The Beckman Institute)
What is Convection?
When a fluid, such as air or a liquid, is heated and then travels away from the source, it carries the thermal energy along. This type of heat transfer is called convection. The fluid above a hot surface expands, becomes less dense, and rises.
At the molecular level, the molecules expand upon introduction of thermal energy. As temperature of the given fluid mass increases, the volume of the fluid must increase by same factor. This effect on the fluid causes displacement. As the immediate hot air rises, it pushes denser, colder air down. This series of events represents how convection currents are formed. The equation for convection rates is calculated as follows:
Q = hc · A · (Ts – Tf)
where Q = heat transferred per unit time; hc = convective heat transfer coefficient; A = heat-transfer area of the surface; Ts = temperature of the surface; and Tf = temperature of the fluid.
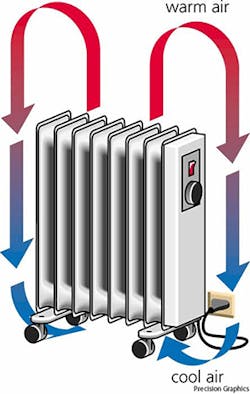
A space heater is a classic convection example. As the space heater heats the air surrounding it near the floor, the air will increase in temperature, expand, and rise to the top of the room. This forces down the cooler air so that it becomes heated, thus creating a convection current.
What is Radiation?
Thermal radiation generates from the emission of electromagnetic waves. These waves carry the energy away from the emitting object. Radiation occurs through a vacuum or any transparent medium (either solid or fluid). Thermal radiation is the direct result of random movements of atoms and molecules in matter. Movement of the charged protons and electrons results in the emission of electromagnetic radiation.
All materials radiate thermal energy based on their temperature. The hotter an object, the more it will radiate. The sun is a clear example of heat radiation that transfers heat across the solar system. At normal room temperatures, objects radiate as infrared waves. The temperature of the object affects the wavelength and frequency of the radiated waves. As temperature increases, the wavelengths within the spectra of the emitted radiation decrease and emit shorter wavelengths with higher-frequency radiation. Thermal radiation is calculated by using the Stefan-Boltzmann law:
P = e · σ · A · (Tr4 – Tc4)
where P = net radiated power; A = radiating area; Tr = temperature of the radiator; Tc = temperature of surroundings; e = emissivity; and σ = Stefan’s constant.
Emissivity for an ideal radiator has a value of 1. Common materials have lower emissivity values. Anodized aluminum has an emissivity value of 0.9 while copper’s is 0.04.
Solar cell or photovoltaic cell, converts the energy of light into electricity via the photovoltaic effect. Light is absorbed and excites the electrcon to a higher energy state and the electric potential is produced by the separation of charges. Efficiency of solar panels has risen in recent years. In fact, those currently being produced by SolarCity, a company co-founded by Elon Musk, are at 22%.
Emissivity is defined as an object’s effectiveness in emitting energy as thermal radiation. It is the ratio, at a given temperature, of the thermal radiation from a surface to the radiation from an ideal black surface as determined by the Stefan-Boltzmann law. Stefan’s constant is determined by constants of nature. The value of the constant is as follows:
σ = (2 · π5 · k4)/(15 · c2 · h3) = 5.670373 × 10–8 W · m–2 · K–4
where k = Boltzmann’s constant; h = Planck’s constants; and c = speed of light in a vacuum.