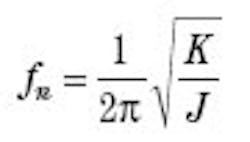One of the major causes of step motor stalling is a phenomenon called resonance. As motors accelerate and decelerate their shafts typically oscillate, causing variations in shaft speed and position, Figure 1. These variations require additional motor torque to quell, thus reducing the available torque for the commanded move. Though at first glance, oscillation torque may seem insignificant, a closer look shows otherwise. In many cases oscillations can sap as much torque as that required for the move. As a result, engineers who follow the rule of thumb and specify a motor with two times the required torque may still be surprised.
What is resonance?
Designers liken step motors to mass-spring systems, Figure 2. The reason is that the magnetic field between rotor and stator behaves like a spring, often producing a resonant response.
Resonance can be defined by two variables: natural resonant frequency fn and the damping ratio ζ. The natural frequency is determined by spring stiffness K and inertia J as follows:
The damping ratio is a dimensionless number that reflects how rapidly transient oscillations decay. The amplitude of a decaying oscillation changes from one cycle to the next by a factor of:
For ζ = 0, the decay factor is 1, and there is no cycle-to-cycle decay. In other words, the system rings endlessly. For ζ between 0 and 1, the decay factor becomes progressively smaller, approaching 0 as ζ approaches 1. When ζ = 1, the decay factor is undefined, and there is no oscillation. Here, the shaft settles to its commanded position without any ringing. For ζ between 0 and 21, the decay factor is greater than 1. This means the ringing increases, and the system is unstable.
In an ordinary step-motor-and-drive system, the viscous coefficients of friction, b1, b2, and b3, are very small, Figure 2.
Furthermore, at medium speed, b1 may become negative, forcing the damping ratio to values near 0 or a negative number. This is the motor’s midrange instability. It is the speed range where the drive provides less than the commanded current, and there is enough oscillation to cause a loss of synchronism in the motor. Designers attempt to solve the problem by increasing the coefficient of friction, b3.
Damping methods
Elastomeric couplings. One way to damp resonance is to insert an elastomer coupling between the rotor and load. If the system starts to oscillate, the coupling b3 will remove energy as the other members of the system oscillate. For good damping, the stiffness of the coupling K2 must be well below that of the motor K1.
The drawback, however, is that the system will be very poor at maintaining position, and the load will be easily disturbed by outside forces. Also, many elastomer couplings become “set” with time and loading, causing the load to change position with respect to the rotor.
Fluid-filled motors. Another damping method is to increase b2 by filling the motor with a viscous ferrofluid. The ferrofluid is magnetic and held in place by the rotor’s permanent magnets. Though this method provides good damping, it comes at the expense of torque at high velocities. Such systems will move smoothly at low speeds, but won’t perform at high velocities.
Viscous dampers. This method uses a comparatively large seismic mass coupled to the rotor via a viscous fluid or elastic solid. The main load remains firmly attached to the rotor, viscous dampers do not sacrifice stiffness. When the load starts to ring, however, the inertia of the solid causes the load to respond sluggishly.
The drawback to viscous dampers appears during rapid acceleration. Typically, machines will run well at high speed, but won’t respond well in accel and decel modes. Also, inertial or viscous dampers are expensive, sometimes costing as much as the motor itself. They require double-shafted rotors and take up significant space.
Active damping. The objective of active damping is to raise the value of ζ by controlling the coefficient b1. To illustate the process, it helps to look at a block diagram, which shows the motor as a selfcontained position loop, Figure 3.
Continue on page 2
To obtain the correct amount of damping required, the system compares the commanded velocity (derivative of Φ) with the actual velocity ω, generating a velocity error, εθ. The damping function acts through the viscous friction coefficient b1, exerting torque on the rotor proportional to the velocity error. Thus, an inner damping (velocity) loop is closed. The end result is a transfer function with a damping ratio determined by:
J is the total system inertia. The next step to understanding how active damping works is to modify the block diagram mathematically so that the feedback and feedforward paths originate and terminate on physically accessible nodes. The mathematics are basic block-diagram algebra.
Figure 4 shows the end result of two operations. First, the terminus of the two paths is moved ahead of K1 to the input (commanded position). Second, the origin of the feedback path is moved to the torque node ahead of the blocks comprising inertia and the first integrator. These two factors now appear in the feedback path. The cascaded inertia and the two integrators have been absorbed into a single block for brevity. The transfer function remains the same; but now the nodes are accessible.
By including a digital tachometer in the drive, commanded velocity can be measured. Motor torque can be obtained by a process completely contained in the drive. These two signals are then differenced and applied to the phase modulator in Figure 4.
Torque sensing comes by way of the drive electronics. Being a feedback mechanism, the active damping “loop” is sensitive to parameters such as stiffness K1, and total inertia J. This is the reason that an antiresonant drive requires coarse adjustment of damping gain based on the particular system. Furthermore, because the feedback mechanism is susceptible to spurious signals at low speeds, active damping can be applied only at velocities above 2 rps.
For more information on antiresonant techniques and drives, circle 331 on the reader service card or log onto Industrial Device’s website at: www.idcmotion.com.
Jack Nordquist is principal electronics design engineer for Industrial Devices Corp., Novato, Calif.