Steady does it: Part 1 of 2
In this installment:
- Passive and active isolation issues
- Isolation system behavior
- Challenges
Increased machine throughput usually requires higher velocities and accelerations, but forces are often limited by the voltage and current restraints of a system's motors and drives. Even if a motor can produce enough power to deliver faster operation, an aggressive motion profile does not necessarily yield higher throughput. In many cases, practical velocity and acceleration are well below maximum achievable values. Why?
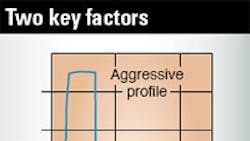
Profile duration, the commanded move time, is only half of the equation. The other part is settling time. Settling time is determined by dynamic effects and can significantly increase when a system makes very aggressive moves. An example is shown in Figure 1.
The problem is even more severe when the settling widow is tightened and higher resolution is required.
To illustrate, the resolution of semiconductor instruments is approaching (and in some cases, going below) 1 nm. Instruments with this resolution are sensitive to even the smallest vibration or disturbance — particularly vibrations excited by the motion profile itself.
The most common vibration mitigation approach is to modify the motion profile by means of trial and error, to keep the entire move and settle duration as short as possible. Often, however, this method is insufficient. Let's explore more effective solutions to address the problem.
Passive isolation
Passive isolation systems are typically used to isolate systems from disturbances transmitted from the floor. They employ a seismic mass supported on a soft spring made of air, metal, or rubber. The spring's damping action absorbs vibrations above the spring's resonance. For this reason, passive isolation manufacturers usually try to lower spring resonant frequency to increase the effective isolation range. The problem is that this makes most passive isolation systems very soft — and softness is detrimental on fast-moving systems such as stages.
When a servo force is applied to a load to generate motion, it also acts on the isolated stationary base, causing it to vibrate. Because the frequency is low (usually below 1 Hz, to 10 Hz) and damping is very light, the isolation system continues vibrating long after the motion profile has ended. See Figure 2 on the previous page.
This vibration acts as disturbance to the servo system, introduces error, and extends the settling time — preventing inspection instruments, to use our example application, from taking measurements.
Active damping
Vibration problems are much less severe with active isolation systems. These, like passive systems, isolate systems from disturbances transmitted to the system from the floor. Active systems detect vibration levels with sensors that send signals into a feedback or feedforward controller, which in turn sends signals to actuators to counteract the forces.
In other words, within the feedback loop, a sensor measures vibrations affecting the isolated base and then the actuator reacts to reduce the level of vibration. So, the active isolation system not only absorbs energy entering from the floor, but also effectively absorbs vibrations generated by the moving stage.
Typical active systems are inherently stiffer than air tables. Their resonant frequency depends on the tuning of their servo, but it is typically higher (greater than 10 Hz) than that of the passive systems — and actively isolated systems are much better damped. As a result, vibration is suppressed more quickly and effectively.
Here is the catch: Most active vibration isolation systems are relatively complex and costly. They are also more difficult to install and their support electronics often require adjustment.
Command feedforward
A simpler and less expensive approach for active damping is the command feedforward method. It is most useful where a known force is applied to an isolated base, and a signal proportional to that force is available.
More sophisticated motion controllers are necessary with this method, as the applied force depends on the stage acceleration determined by the motion controller.
Here's how it works: An analog signal (proportional to the commanded acceleration in a certain direction) is sent by the motion con- troller to an actuator, which in turn produces force equal in magnitude but opposite in direction. Typically, additional analog signals (indicating the commanded position) are also sent. They account for the effects of coupling twist: An isolated base twists clockwise if there is X acceleration when the stage is in full -Y position, and counterclockwise when the stage is in full +Y position.
Besides being more cost effective than sensor-based isolation systems, command feedforward cannot become unstable, and significantly improves settling performance. One caveat: Command feedforward also requires setup and proper tuning of the feedforward gains.
Modeling isolation system vibration
Active isolation systems, even when well tuned, cannot eliminate vibration entirely — and to reiterate, semiconductor inspection machines can use very high-resolution feedback devices and are extremely sensitive to even the slightest disturbances, which can extend settling time to nanometer or sub-nanometer settling windows.
Let's explore another option. Consider isolation-system vibration of the model shown in Figure 4, which depicts a direct-drive system on a base with limited mass and stiffness.
The feedback reading is relative to the base:
Xencoder = XL - XB
The force is applied both on the load at the stationary base.
The transfer function describing the relation between the applied force and feedback reading is:
The part in the parentheses represents isolation system dynamics, with parameters:
ML = Total mass of load
MB = Isolated stationary base mass
F = Applied force
XL = Load displacement relative to ground
XB = Base displacement
K = Stiffness of isolation system
d = Damping of isolation system
Two possible solutions exist:
-
Increased disturbance rejection of the servo system
-
Special motion profiles that do not excite disturbing vibrations
One method to improve the servo disturbance rejection is frame acceleration compensation. The performance of a stage with passive isolation can be upgraded by using two accelerometers in XY directions. The acceleration of the base is measured in each direction, and a compensation force (ML × a) is applied to the drive command — such that the resulting position error is significantly reduced as shown in Figure 5.
This method does not prevent isolation-system vibration, but does minimize the relative move between bases and loads — beneficial because inspection instruments are installed on bases.
Tune in for the second part of this series next month, when we'll review frequency domain behavior, disturbance- rejection algorithms, and another approach using input shaping.
We'll also study a new class of controls, executed as special functions on motion controllers, that minimizes the effect of isolation-system vibrations on settling time.
For more information, email [email protected] or visit acsmotioncontrol.com.
Consider the plight of motion system designers in the semiconductor industry, who face constant demand for higher performance — to produce more semiconductors, faster, and at a lower cost. This makes for significant challenges. To illustrate, one aspect of the semiconductor manufacturing process, inspection, usually involves positioning silicon wafers relative to optical (or other) components by placing the wafers on a fast-moving XY stage. How can this delicate operation be sped up with accuracy? Part of the answer, which we cover here, is in mitigation of vibration. Whether you work in the semiconductor industry or another field, controls-based damping could help your design move more nimbly.
Two key factors
Settling time is determined by dynamic effects and it increases when a system moves aggressively. Left: Two velocity profiles for the same moving distance. Right: Their servo position error. Though the blue profile has significantly shorter duration, it generates higher position error and results in longer settling time. Total move and settle time is much shorter with the less aggressive profile.
Extended ringing
When force is applied to a load to generate motion, it also acts on the isolated stationary base, causing it to vibrate. Low frequency and light damping contribute to isolation system vibration, even long after motion has ceased. This vibration acts as a disturbance to the servo system, introduces position error, and prolongs settling time.
Move time vs. settling time
Move time is the duration of the motion profile. It is dominated by commanded motion parameters such as velocity and acceleration. Settling time is the duration of time from when the profile ends until the system reaches and stays within a certain target window. The sum of move plus settle times is what determines a system's agility. That is why for applications with point-to-point moves, machine throughput is affected and expressed in terms of move and settle.
Isolation system model
The effect of the isolation system vibration can be described using a basic model. A direct drive system is mounted on a base with limited mass and stiffness. Force is applied on the load at the stationary base.
Frame acceleration compensation control scheme
Base acceleration is measured in each direction and a compensation force ML × a is applied to the drive command, such that resulting position error is significantly reduced (ML - moving load mass). This does not prevent isolation system vibration, but minimizes relative movement between the base and load.