Machinedesign 7582 Hidden F Loads Promo 0

Fastening & Joining

Calculating the Hidden Loads in Fasteners Near Edges

July 6, 2016

Fasteners installed near the ends or edges of load-carrying members often have hidden loads greater than the actual applied load.

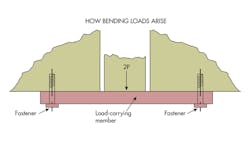
Fasteners installed near the end or edges of load-carrying members often carry more than just the applied load. They also carry a hidden load generated by bending moments in the load-carrying member. This additional load may outweigh the applied load by a great deal.

Machinedesign Com Sites Machinedesign com Files Uploads 2016 07 06 Hidden F Loads 1

When a central, load (2P) is imposed on a load-carrying member that is fastened near both ends, the ends of the member tend to curve up. Restraints imposed by abutting member create bearing loads that add to the load carried by the fasteners. Such bearing loads may be significantly greater than the applied load.

If the load–carrying member in the image below were infinitely rigid, the fastener would be required to resist only the applied 2P. But in most applications, a different loading condition develops. The flexibility of the load-carrying member typically demands that is edges or ends resist angular rotation caused by local loads.

For this analysis, bearing loads are assumed to be at a maximum at the edges, tapering to zero at the fastener centerline with a triangular load distribution. Under these conditions, fastener loads and stress are from:

σ_max = 24sm/(8ws³ – 4R³)

P₁ = σ_max/6s(3ws² – 4R³)

Machinedesign Com Sites Machinedesign com Files Uploads 2016 07 06 Hidden F Loads 2

A 5-in-wide bar is centrally loaded with a force of 10,000 lb. The distance between fastener centerlines is 36 in and the bar extends 2 in beyond the fastener centerline at each end.

To use these equations, M, the resistive moment created by the bearing load, is conservatively set equal to the bending moment needs to maintain a fixed-end constraint of the load-carrying member. Then the first equation determines the maximum bearing stress and the second equation determines the resultant bearing load on the fastener.

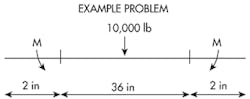
Example: A 5-in wide bar is centrally loaded by a force of 10,000 lb and restrained at each end by a fastener passing through a hole with a radius of 0.5 in. The distance between the holes’ centerline is 36 in and the distance between the fastener centerline and the bar end is 2 in. What are the maximum bearing stress and maximum load on the fasteners?

From elementary strength of materials,

M = 2PL/8 = 10,000(36)/8 = 45,000 in-lb

Then maximum stress is found from the first equation as:

σ_max = 24(2)(45,000)/[8(5)(2)3 – 3π(0.5)4
= 6,800 psi

The bearing load, from the second equation, is then:

P₁ = 6,800/6(2) [3(5)(2)2 – 4(0.5)3]
= 33,700 lb

The maximum load on the fastener is thus the bearing load plus half the applied load, or 38,700 lb.

Nomenclature:

L is the distance between fastener centerlines, in.
M is the resistive moment provided by the bearing load, in-lb.
P is half of the total load on the load bearing member, lb.
P₁ is the resultant bearing load on the fastener, lb.
R is the radius of the fastener holes, in.
s is the distance from the fastener centerline to the end of the load carrying member, in.
w is the width of the load carrying member, in.
σ_max is the maximum bearing stress, psi.