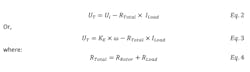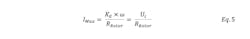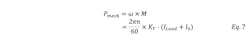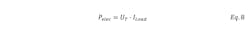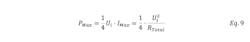Design engineers know that both brush DC and brushless DC (BLDC) motors can operate as generators, but many tend to avoid running brushed DC motors in generating mode because they believe it is inefficient. Unfortunately, by avoiding using brushed DC motors as a generator, engineers pass up several significant benefits.
For example, brushed DC motors are less expensive than miniature generators even though they both perform the same function. Brushed DC motors also offer a wide range of options to address specific application needs. And brushed DC motors are particularly well-suited for applications that require voltage as an input without a power source, such as door locks and small energy harvesters. When these benefits are considered and certain engineering concepts are applied to the decision, brushed DC motors can be attractive and efficient options as generators. Here is an overview of the basic relationships between speed, voltage, torque and current when using brushed DC motors as generators.
Basics
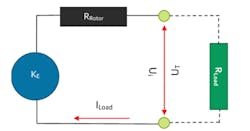
As a motor’s rotor rotates through a magnetic field, the electromotive force induces a voltage on the rotor windings. This is called the “back EMF,” and a motor’s back EMF constant, KE, (given in mV/rpm), can be found on its specification sheet. The back EMF (Ui) is directly proportional to the motor shaft rotation’s angular speed (ω) is calculated using:
When operating a motor as a generator, the shaft is mechanically coupled and rotated by an external source, which makes the rotor’s coil segments rotate through a sinusoidally varying magnetic flux in the air gap. Each turn of the rotor winding is induced with sinusoidal voltage, with the rotational speed and magnetic flux linkage determining the voltage magnitude. For instance, if a rotor coil consists of one turn, the induced EMF is sinusoidal with a period equal to one electrical cycle.
By design, brushed DC rotors are wound in odd numbers of segments (3,5,7, etc.) and supplies power to the coils through a pair of brushes. When the shaft rotates in generation mode, the generated back EMF voltage is measured at the output terminals. Based on the motor’s properties, which includes the number of coil segments, voltage ripple is typically present and generally represents less than 5% of the output voltage.
The output voltage is a function of shaft speed, so the back EMF constant (KE) should be selected to satisfy Eq. 1 when selecting motors to be used as generators. Without considering the load, the back EMF constant of the winding should be larger than ωUi . If the achievable shaft speed does not reach a sufficient back EMF, a suitable gear reduction can be added to increase the speed at motor shaft if the motor’s maximum permissible speed parameters are not exceeded.
Terminal Voltage, Maximum Current & Load Resistance
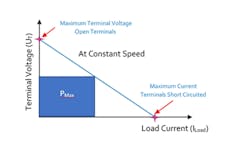
The graph above shows that the voltage generated across the motor’s terminals (UT) is directly proportional to the angular speed of the rotor when the load (RLoad) is not connected across the terminals. In this condition, the current through the motor is zero. When a load is connected across the motor terminal, current flows and the voltage is reduced depending on the total load resistance. The terminal voltage (UT) when the load is connected and current (ILoad) is flowing through the circuit is given as:
As the load current increases for a fixed angular speed of the motor shaft, the terminal voltage decreases. When the back EMF equals the resistive voltage drop across the terminals, the terminal voltage becomes zero.
The graph above charts the load current versus terminal voltage of an ideal brushed DC motor used as a generator. When motor terminals are not connected, UT equals Ui, and current does not flow through the rotor windings. When the terminals are short-circuited, the maximum amount of current flows through the circuit and UT becomes zero.
The maximum current through the circuit can be calculated as:
With all other parameters held constant, as the motor shaft’s angular speed increases, the graph shifts right with same slope, increasing both Ui and IMax. In the above equation, the motor windings’ inherent resistance (RRotor) is the limiting factor for the generator mode’s maximum current. If RRotor is high, the generator’s sensitivity increases and the resulting voltage varies with current drawn creates, creating an unstable system. A motor with a higher back EMF constant and lower resistance, however, provides stable operation.
Driving Torque & Power Balance
When a motor is driven in generator mode with open terminals, no current flows through the circuit and mechanical friction creates losses in the driving unit. This condition is similar to unloaded motor operation.
The torque (M) equation for a motor is given as:
where: KT = Motor Torque Constant (mNm/A) I0 = No load current of the motor (A).
The generator must be driven with a torque that will generate the required load current through the winding when the terminals are closed across the load resistor (RLoad). Motor selection is limited by the maximum amount of torque that can be applied on the shaft in generator mode. Brushed DC motor operation is limited by the maximum continuous torque (thermal and mechanical) and maximum continuous speed (mechanical and electrical) available. Selecting a motor that can handle the generator’s torque on the shaft and manage the maximum current through its circuit is like the process of sizing motors based on desired load points.
At steady state, the mechanical input power to the generator can be represented as:
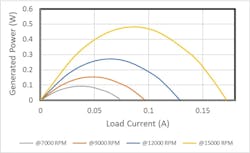
The electrical output power at any load current and terminal voltage can be represented by the rectangular area under the slope as shown in Figure 2: Load Current Versus Terminal Voltage Graph.
Output power maxes out when UT is half of the Ui. At this point, the load current ILoad is half of the maximum current IMax.
Therefore,
A motor used for a generator should not be chosen solely on power considerations. Ideally, PMax should always be higher than the generator’s required electrical output power. Depending on the load current value, the load point on the Figure 2 graph can move along the x-axis. Thus, the actual power output (PActual), may be less than PMax. While selecting the right motor to be used as a generator, PActual should be taken into consideration and not PMax. This may require selecting a motor with a higher rating.
The efficiency of the generator can be determined as:
Selecting a Motor as a Generator
Example 1: This example reviews the selection of a Portescap Athlonix series DC brush motor for a generator application. The back EMF constant of the Athlonix series 17 DCT with 209P coil is 1.17 mv/rpm. The motor’s characteristic curves are plotted in Figure 3. If this motor is used as a generator at 5,000 rpm of shaft speed, the output back EMF would be 5.85 V (Eq. 1).
The maximum load current through the circuit under short-circuited condition would be:
This value of IMax. exceeds the motor’s maximum continuous current (0.55 A). This may be acceptable for intermittent operation, which is determined by the motor’s thermal time constant and expected duty cycle. For continuous generator operation, however, a load resistance (RLoad) is recommended using the equation:
where ICont is the motor’s maximum continuous current.
So, if a load resistance that exceeds 3 Ω is used in the generator, the 209P coil is good for input speeds up to 5,000 rpm. If load resistance cannot be used due to mechanical or technical limitations, or if the input speed is higher than 5,000 rpm, another coil should be chosen. For example: the 211P coil may be a better choice for this requirement.
Example 2: The back EMF of the Portescap 16C18 motor with a 205P coil is 0.70 mV/rpm. At 10,000 rUnder short-circuited condition, the maximum current that can flow through the windings is:
which is less than the motor’s maximum continuous current (ICont). Therefore, using this motor as a generator at 10,000 rpm of shaft speed is acceptable without considering an external resistance load.
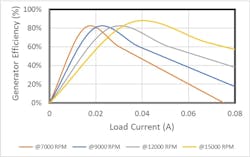
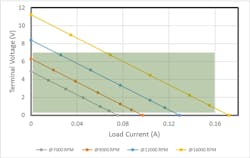
The output characteristics for 16C18 at different shaft speed is plotted in below.
The shaded box in the graph above is the area of continuous operation. For intermittent operations, various factors such as maximum temperature rise, maximum shaft speed, the motor’s mechanical limit, and generator life should be considered.
The above graphs show that the 16C18’s efficiency is relatively higher at lower generator current. At maximum output power, the output efficiency is close to 50%. It is ideal to select a generator with a working point close to the maximum efficiency. This ensures system losses are minimized and less mechanical input power is needed to generate the desired output voltage and-current characteristics.
It is often misunderstood that a brushed DC motor running in generating mode is not as efficient as when functioning as a motor. However, using the proper motor, loads and operating speed will yield reasonably high efficiencies. The electrical and mechanical factors must always be considered when determining operating points. Knowledgeable application engineers with extensive design experience are available for consultation to select the correct motor for a range of applications.
Sunil Kedia is the Core Market New Product Development Manager at Portescap.