Optical encoders accurately track the rotational position of shafts over a dynamic range. In a machine tool, that position data results in better spindle speed control, which can improve surface finishes and reduce secondary operations. However, to obtain the best accuracies from these devices, designers need to avoid several common pitfalls.
Taking a pulse
Speed control requires that designers reference the optical encoder's output signals to a time base. This is usually done in one of two ways: detecting two consecutive pulses and measuring the time between them, or counting a series of data pulses for an increment of time and averaging the pulse rate over that interval.
For example, in the consecutive pulse method, suppose we have an encoder with a resolution of 360 cycles/ rev and a measured time between two pulses of 100 μsec. The instantaneous rotational speed, in rpm, is calculated as 60 divided by the product of the resolution (360) and the time interval (0.0001 sec) for a result of 1,667 rpm.
This seems straightforward but there are limitations, especially in PID control systems and phaselocked servos. These systems anticipate the timing of subsequent pulses. Therefore, any timing-related errors can cause them to hunt, resulting in an inefficient and noisy drive.
Also, consecutive pulse timing requires the servo to "dead reckon" position between counts, but this becomes more difficult if quadrature detection is used. Any symmetry or quadrature errors will feed back into the servo loop.
A better method is for the controller to use leading-edge-to-leading edge detection, since it is inherently more accurate. Ideally, the controller should detect these pulses asynchronously, but this requires a more complex signal processing scheme.
Thus, except for specialized systems, a more practical method is to use a pulse counter and a timer, which offers several advantages. For one, many encoder input stages on PLCs already incorporate a pulse counting feature. Therefore, engineers can easily write software code to periodically poll the counter, subtract the current reading from the previous reading, and calculate the speed based on the time between the two counting events.
Using the same encoder resolution as in the previous example, let's say that the counter records 101 pulses in 10.2 msec. The average rotational velocity over that time is calculated by multiplying 60 times the number of pulses and dividing that answer by the product of the resolution and time for a result of 1,650 rpm. Note that in the earlier example we calculated instantaneous velocity. In this example we calculated the average velocity. Because you need lots of counts to stabilize a velocity or position control loop, this method is better suited to most of the common control systems.
Another advantage is that while it's possible to have an error of up to one count, which can happen if the counter is polled just before it registers an incremental count, this count is not lost. Instead, it shows up in the next timed interval. These counting errors are not cumulative as the encoder always returns 360 counts over the course of a complete revolution.
In these examples, we treated a complete cycle of the A channel as a single pulse on the counter. Most encoder input circuitry has the option of quadrature detection to count the up and down transitions on both the A and B channels. In effect, this multiplies the input signal and reduces the speed error from pulse counting by a factor of four.
Once around
The index is a once-per-revolution signal usable for both error detection and safety. A number of index schemes are available, here is one of the more popular ones. It is described as a 1/2-cycle index, gated with negative B. The index pulse is ANDed with the negative part of the B cycle to ensure that the indexpulse duration and location bear a precise relationship to the B cycle.
An opportunity to establish a precise reference occurs when the index pulse changes from LO to HI. Monitoring that transition on the A channel at that moment gives a precise location regardless of the rotation direction. But monitoring the index transition only is insufficient because it occurs at a different part of the cycle depending on whether the encoder turns clockwise or counterclockwise.
Continue on page 2
Use of the index mark for error checking is fairly common. The system reads the indicated counts on a separate index counter circuit and compares it to the known resolution of the encoder. Electrically noisy environments can lead to spurious counts. Similarly, working near a system's bandwidth or speed limits can reduce the apparent counts.
Because the index mark monitors counts on a once-per-revolution basis, it's easy to quickly overrun a counter. Therefore, it's good practice to subtract a fixed number of counts periodically based on speed to reset the counter. Other reset schemes involve zeroing the counter at every nth index pulse.
Fail-safe
Whether you use this scheme or another, be sure to include several fail-safe procedures. Comparing the counts in the index counter to the known resolution, for example, can be used to shut down the system when the disparity gets too great. A large disparity may occur with a loss of any channel from an intermittent or broken connection.
Another fail-safe method, used with position control systems, is to track encoder counts to prevent a limit switch overrun. If the limit switch fails to actuate yet the system has been tracking encoder turns, it can safely shut down before any damage is done.
And a one, and a two, . . .
Using quadrature is not only convenient for multiplying the apparent data rate from the encoder, it is also a means of detecting direction. Industry uses the conventions of clockwise or counterclockwise positive pretty much equally. Most controllers accommodate either type of input. Since the A and B cycles are offset by 90 degrees (1/4 cycle, hence the term quadrature), the input must rotate a maximum of 1/4 cycle before detecting the rotation direction. This is most important during system start-up because systems already running cannot change direction instantaneously.
Quadrature is also useful in stabilizing systems intended to turn in only one direction. A system at rest can dither on a logic transition caused by mechanical vibration. A counter using one channel sees this as real motion, causing errors or a controller fault. But a quadrature counter looks at both the A and B channels and can distinguish dither from true rotational motion.
Frequency counts
When choosing encoder resolution, it's important to look at the system data rate. For example, a counter may have a bandwidth of 100 kHz. With a 1:1 coupling between the encoder and the drive mechanism and a maximum speed of 3,200 rpm, the maximum encoder resolution is 1,875 counts per revolution–bandwidth multiplied by 60, the result of which is divided by the maximum speed.
Because it's poor practice to operate a system at the design limit, a rule of thumb is to use about 80% of the calculated value, or 1,500 cycles per revolution. If you need a minimum of 30 pulses between counts, for instance, then a sample rate of 375 μsec would do the job. Allow some overhead in the sample rate if signal error-checking is part of the sample scheme.
The approach works well for encoders with moderate resolutions. For high resolutions, it's best to consult with the manufacturer for specific recommendations. For systems that run cyclically rather than at constant speed, it may make sense to vary the sample rate depending on the acceleration profile and the tolerance for speed error.
And don't forget to provide for catastrophic failure. The power supply to the encoder could be interrupted or the coupling mechanism could fail, resulting in a complete loss of control. In some instances it may make sense to modify the sample rate to an interval representing the maximum allowable time that the system can operate open loop.
Mechanical resonances
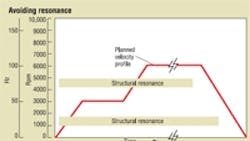
With a closed-loop servo control system, you must take into account the mechanical factors associated with the drive mechanism. It is standard practice to accommodate inertial loads, cycle times, and power requirements. Another factor - often missed - is the mechanical resonance in the system.
The affects of resonance can dramatically effect drive performance, and in the extreme can cause instability. If the system operates over a range of speeds, it's more likely to encounter undesirable resonance than in constant speed operation.
Designers should assess all physical elements in the control loop to determine whether a characteristic frequency will overlap with the drive speed. Mechanical couplings, drive belts, gear trains, conveyors, even fairly large drums can exhibit resonances that will feed back into the control loop.
Component manufacturers can supply data on the characteristic frequencies of these elements. These can be plotted on a graph with drive speed on the y axis and the desired operating profile of the drive overlaid on a time scale. You can then assess whether to modify the drive's operating envelope, choose different components, or provide some other mechanical means, such as dampers, to reduce the resonance effects.
Continue on page 3
A closer look at optical encoders
Incremental and industrial optical encoders mechanically couple to rotating shafts and produce a series of pulses that bear a linear relationship to the shaft rotation. Each encoder's resolution determines the proportionality of that relationship.
The heart of an optical encoder is its code disk. It is usually made of a clear material and contains a series of radial "spokes," which are the opaque areas created through a photolithographic process. The disk affixes to a spindle that rides on a dual bearing assembly. This arrangement minimizes runout.
To obtain signals, an LED light source shines through a mask onto the code disk and impinges on a photocell array. The mask acts much like the shutter in a movie camera.
The code disk, mask, and photocell array produce three types of data output: the "A" or primary disk resolution track; the "B" or quadrature code track; and "Z" an index pulse that is a once-per-revolution signal. Output signal quality depends on the alignment of the optical elements with the code disk, the stability of the disk, and the responses of the photocell and attendant electronics. Bandwidth is limited primarily by the response of the photocell and secondarily by the signal conditioning electronics.
The complementary signals - A, B, and Z - are usually created by running the primary signals through an inverter. They can exclude noise through a technique referred to as common mode noise rejection where a differential line receiver or comparator takes a signal and its complement and essentially subtracts the two.
With perfect signals, the difference produces sharp transitions at the signal switching points. Any common mode noise on the encoder data lines, from radiated or induced electrical fields for example, shows up as a noise spike that is virtually identical on both the primary signal line and its complement. A comparator subtracts this spike for a clean signal. The differential input essentially ignores the noise spike and reliably detects the count.
In the real world, the signal shape usually deviates somewhat from the ideal "square" shape in a few predictable and not so predictable ways. For example: high capacitance on the output lines can cause indistinct HI/LO transitions. Noise from motor power lines can induce noise into encoder signal lines when run in the same cable tray.
Usually these influences are minimal, but any good system design uses proper cabling practice and differential line receivers to account for these possible sources of signal corruption.
Scott Orlosky, P.E., is the Sales and Marketing Manager at BEI's Industrial Encoder Division, Goleta, Calif. He wishes to acknowledge the assistance of Aram Soghikian of TQ Automation in San Leandro, Calif., for his contributions to this article.